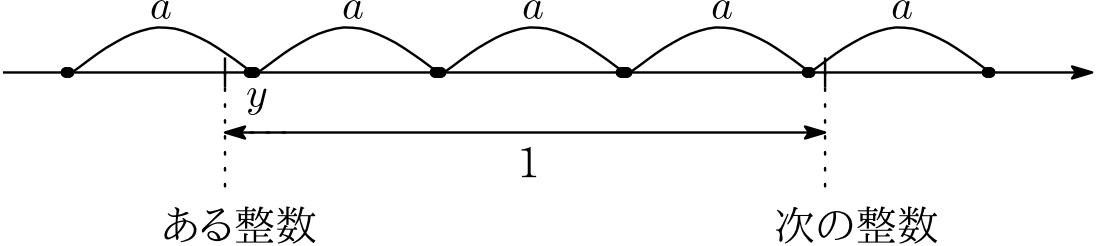
また，いくつかの具体的な $n：0,1,2,3,\cdots$ について“実験”してみることも，$f(n),g(n)$ の構造を把握する上でとても有効です．
$\smkk{解答}$ $a=\log_{10}2(=0.30103)$ とおくと \begin{align*} \log_{10}{2^n}=n\log_{10}2=a\cdot n\ . \end{align*} (1) \begin{align*} \log_{10}2^{2018}=&2018\log_{10}2\\ =&2018\cdot a\\ =&607.47854\\ =&\underbrace{607}_{整数部分}+\underbrace{0.47854}_{小数部分}\ .\ \cdots①\\ \thr\ 2^{2018}=&10^{607+0.47854}.\ \cdots② \end{align*} ここで \begin{align*} \underbrace{\log_{10}3}_{0.47712}\lt 0.47854\lt \underbrace{\log_{10}4}_{2a=0.60206} \end{align*} だから，②より \begin{align*} &10^{607+\log_{10}3}\lt 2^{2018}\lt10^{607+\log_{10}4}.\ \cdots③\\ &3\cdot 10^{607}\lt 2^{2018}\lt 4\cdot 10^{607}.\ \cdots③' \end{align*} よって \begin{align*} f(2018)=\boxed{608}^{アイウ},g(2018)=\boxed{3}^{エ}. \end{align*} (2) (1)からわかるように，$\log_{10}2^n$ の整数部分を $p$，小数部分を $q$ とするとき， \begin{align*} &\lbrc{ 2^n\ の桁数は\ p+1.\\ \log_{10}l\leqq q\lt\log_{10}(l+1)\ を満たす整数 \ l \ が 2^n\ の首位. }\quad\cdots(★) \end{align*} これ以降は，この(★)に基づいて解答する．
\begin{align*} \log_{10}{2^{10k}}=&10k\cdot a\\ =&3.0103\times k\\ =&3k+\underbrace{0.0103\times k}_{\alpha\,とおく}\ ,\ \cdots④\\ \log_{10}{2^{10k+3}}=&(10k+3)\cdot a\\ =&3k+0.0103\times k+3a\\ =&3k+\underbrace{0.0103\times k+0.90309}_{\beta\,とおく}\ ,\ \cdots⑤\\ \log_{10}{2^{10k+9}}=&(10k+9)\cdot a\\ =&3k+0.0103\times k+9a\\ =&3k+0.0103\times k+2.70927\\ =&(3k+2)+\underbrace{0.0103\times k+0.70927}_{\gamma\ \,とおく}.\ \cdots⑥ \end{align*} ここで，$0\leqq k\leqq 9$ より \begin{align*} 0\leqq&\alpha\leqq 0.0103\times9=0.0927\lt1,\ \cdots④'\\ 0.90309\leqq&\beta\leqq 0.0927+0.90309=0.99579\lt1,\ \cdots⑤'\\ 0.70927\leqq&\gamma\leqq 0.0927+0.70927=0.80197\lt1.\ \cdots⑥' \end{align*} つまり，④，⑤，⑥において，$\alpha,\beta,\gamma$ は小数部分であり，それぞれの整数部分は $3k\ ,\ 3k\ ,\ 3k+2$ である．よって \begin{align*} f(10k)=^{オ}\boxed3k+\boxed1^{カ}\ ,\ f(10k+3)=^{キ}\boxed3k+\boxed1^{ク}\ ,\ f(10k+9)=^{ケ}\boxed3k+\boxed3^{コ}. \end{align*} 次に，小数部分をもとに首位を求める．④$'$ より \begin{align*} &\log_{10}1\leqq\alpha\lt\log_{10}2.\\ \thr\ &g(10k)=\boxed1^{サ}. \end{align*} ⑤$'$ において，$0.90309=3a=\log_{10}8$ だから \begin{align*} &\log_{10}8\leqq\beta.\\ \thr\ &g(10k+3)=\boxed8^{シ}\ ,\ \boxed9^{ス}. \end{align*} ⑥$'$ において， \begin{align*} \lbrc{ \log_{10}5=1-a=0.69897\lt 0.70927,\\ 0.80197\lt 0.84510=\log_{10}7 } \end{align*} だから \begin{align*} &\log_{10}5\lt\gamma\lt\log_{10}7.\\ \thr\ &g(10k+9)=\boxed5^{セ}\ ,\ \boxed6^{ソ}. \end{align*} (3) まず，
なお，以下においては，$f(n)$ が連続して同じ値をとる $n$ の連なり(例えば $n=0,1,2,3$ )を「連続部分」と呼び，連続部分となる $n$ の個数を「長さ」ということにする．
以上で，$(\ast)$ が示せた．
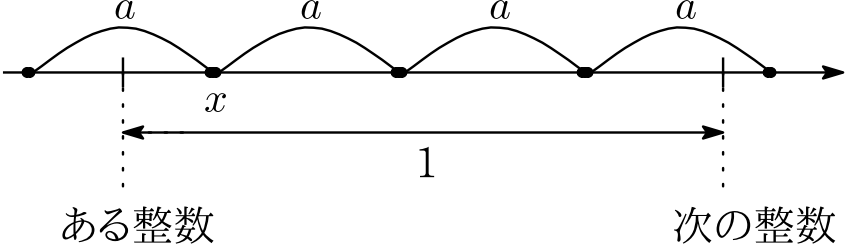
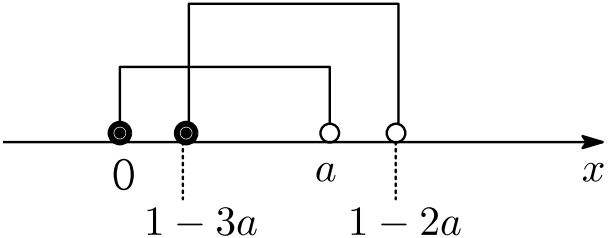
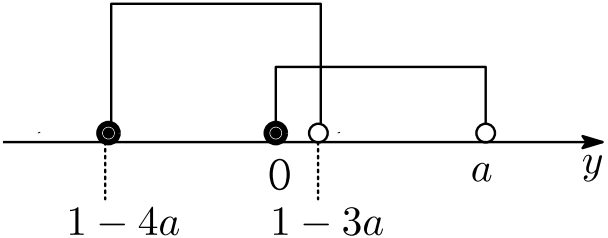
これらと(☆)より，求める $g(n)=4$ となる $n$ の個数は \begin{align*} x=\boxed{196}^{タチツ}. \end{align*}
$\smkk{解説}$
まずは，「対数」の定義の確認から．
\begin{align*}
\log_28
\end{align*}
の値は何だかわかりますか？そう，「3」ですね．大切なのは，その求め方です．
\begin{align*}
&\log_28 とは\ ,\ 2^{\boxed{\phantom a}}=8\ の\boxed{\phantom a}に入る値のこと．\\
&よって，\log_28=3.
\end{align*}
これが，対数の定義に基づいた正しい求め方です．こうしないで，次のようにしてはいけません！(悪いことを書きますから，あまりよく見ちゃダメですよ～)
$\hskip-40mm\log_28=\log_22^3=3\log_22=3\cdot 1=3.$
こんな風に，「定義」そっちのけで「定理・公式」だけを暗記してやり過ごしてしまうと，先々いろんなことが理解できなくなってしまいますよ～．
もちろん，定義を理解した上で，対数の公式を用いて
\begin{align*}
&\log_{10}2\cdot3=\log_{10}2+\log_{10}3,\\
&\log_{10}2^3=3\log_{10}2
\end{align*}
のように計算できるようにもしなければなりませんが．
ちなみに，③を③$'$ にする際には次のように計算しています．
\begin{align*}
10^{607+\log_{10}3}=&10^{607}\cdot \uliner{10^{\log_{10}3}}\\
=&10^{607}\cdot \uliner3.
\end{align*}
ここで，下線部2か所が等しいことがわからない生徒さんが続出する訳ですが・・・(苦笑)
\begin{align*}
&\log_{10}3 とは\ ,\ 10^{\boxed{\phantom a}}=3\ の\boxed{\phantom a}に入る値のこと．\\
&よって，\boxed{\phantom a} へ\log_{10}3を代入して，10^{\log_{10}3}=3\ .
\end{align*}
あたり前でしたね．要するに，対数の定義を理解し，反復練習によってそれを身につけていれば，こうしたこともスッと頭に入るのです．逆に，対数の定義があやふやなままでは，今後，何も習得することはできません．
次に，本問のテーマ：「常用対数と桁数，首位」に関する常識の確認を．次の表を見てください．(ここでは簡単のために $\log_{10}2=0.3$，$\log_{10}3=0.48$，$\log_{10}7=0.85$ としています．)
\begin{align*}
&\begin{array}{c||c|c|c|c|c|c|c|c|c}
m\ (1桁)&\phantom01\phantom0&\phantom02\phantom0&3&\phantom04\phantom0&\phantom05\phantom0&6&7&\phantom08\phantom0&9\\
\hline
\log_{10}m&0&0.3&0.48&0.6&0.7&0.78&0.85&0.9&0.96 \end{array}\\
&\begin{array}{c||c|c|c|c|c|c|c|c|c}
m\ (2桁)&10&20&30&40&50&60&70&80&90\\
\hline
\log_{10}m&\phantom01\phantom0&1.3&1.48&1.6&1.7&1.78&1.85&1.9&1.96 \end{array}\\
&\begin{array}{c||c|c|c|c|c|c|c|c|c}
m\ (3桁)&100&200&300&400&500&600&700&800&900\\
\hline
\log_{10}m&2&2.3&2.48&2.6&2.7&2.78&2.85&2.9&2.96
\end{array}
\end{align*}
これを見れば，$m$ の桁数が一定の部分では常用対数の整数部分も一定であり，常用対数の小数部分が大きいほど首位も大きくなっていることがわかりますね．常用対数を「学ぶ」とは，こうした「関係性」を知り，理解することです．
なお，例えば $m=600$ の常用対数の値は，次のように計算しています(他も同様)．
\begin{align*}
\log_{10}600=&\log_{10}2\cdot3\cdot10^2\\
=&\log_{10}2+\log_{10}3+2=2.78\ .
\end{align*}
さて，(1)は，常用対数を用いて桁数と首位を求めるという典型的な問題ですが，ナメてはいけません！この「典型問題」を「正しく」学んでいるかどうかで，上へ行けるか否かが決まります．
$\smkk{着眼}$ でも書いたように「桁数を $d$ とおく」などという“逃げ”の姿勢をとってはなりません．で見た「関係性」に注目し，さっそく $\log_{10}2^{2018}$ の値(①式)を求めます．その後の②式は，「$2^{2018}$ という目標」を「$\log_{10}2^{2018}$ という手段」を用いて表した式であり，実に自然なものです．
これで $10^{607}\lt 2^{2018}\lt 10^{608}$ がわかったので桁数はOK．そこで，次に首位を求めるために， $\log_{10}2^{2018}$ の小数部分 $0.47854$ について考えます．この値は，問題文で与えられた $\log_{10}3=0.47712$ よりわずかに大きいですから， $\log_{10}3$ および $\log_{10}4$ と比べます．
これで，$2^{2018}$ 自身の値に関する不等式③および③$'$ が得られました．③$'$ の左辺：$3\cdot10^{607}$ は
\begin{align*}
3\,\underbrace{\,0\,0\,0\,\cdots\,0\,0\,}_{0\ が\ 607\ 個}
\end{align*}
つまり，首位が 3 で桁数が 608 である自然数の中で最小のものです($4\cdot10^{607}$ についても同様)．これで，(1)は完了ですね．
このように，(1)の $\smkk{解答}$ では，常用対数の値①をもとに $2^{2018}$ 自身の値に関する不等式 ③$'$ を作って答えを書きましたが，上記の「関係性」を知っている者としては，①の後は
\begin{align*}
&桁数は，整数部分に 1 を加えて 608,\\
&首位は，小数部分が\log_{10}3 と \log_{10}4 の間だから 3
\end{align*}
で片付けたい，というのが本音です．だってこれは「常用対数」に関する「常識」なんですから！ただ，これだけでは「説明不足」とされる心配もあるので，$\smkk{解答}$ では“いちおう”詳しく書いておいたのです．
ただし，問題のレベルがアップする(2)以降では，の「関係性」を既知とする立場で解答しないと大変です．そこで，$\smkk{解答}$(2)の冒頭で，(★)に基づいて桁数，首位を一気に直接求める立場をとることを明確に宣言しました．(1)において，「関係性」に関する詳しい説明を一度しているので，(2)以降では省いても許されるのが通例だと思われます．
なお，②から③を得る際，厳密には，底：10 が 1 より大きいので
\begin{align*}
&607+0.47854\ と\ 607+\log_{10}3\ の大小が\\
&10^{607+0.47854}\ と\ 10^{607+\log_{10}3}\ の大小と一致する
\end{align*}
ことを用いています．指数や対数の大小を論じる際には，「底と $1$ の大小関係」に関する注意が欠かせませんでしたね．
(★)を既知とする立場をとれば，④⑤⑥式のように常用対数の整数部分，小数部分が一目でわかる形を作れば，(2)は“即答”ですね．その際，もちろん $0\leqq k\leqq9$ であることに留意せねばなりませんが．
さて，いよいよ(3)です．(1)，(2)の活かし方がすぐにわかる人はそれでよいとして，そうでない人は・・・，$\smkk{着眼}$ で書いた「実験」をしてみましょう．
\begin{align*}
〔表＃〕\ \begin{array}{c|c|c|c|c|c|c|c|c|c|c|c}
n&0&1&2&3&4&5&6&7&8&9&\cdots\\
\hline
2^n&1&2&4&8&16&32&64&128&256&512&\cdots\\
\hline
f(n)&1&1&1&1&2&2&2&3&3&3&\cdots\\
\hline
g(n)&1&2&\uliner4&8&1&3&6&1&2&5&\cdots
\end{array}
\end{align*}
$f(n)$ については一目瞭然ですね．「$1,1,1,1$」，「$2,2,2$」，「$3,3,3$」のように，同じ値が何回か連続して現れます．まあ，言われてみれば当たり前ですが．
こうした“現象観察”をした上で(2)の結果を見直せば，その意味が手に取るようにわかるはずです．
\begin{align*}
&\begin{array}{c|c|c|c|c|c|c|c}
n&10k&10k+1&10k+2&10k+3&10k+4&\cdots&10k+9\\
\hline
f(n)&\uliner{3k+1}&3k+1&3k+1&\uliner{3k+1}&&\cdots&\uliner{3k+3}\\
\hline
g(n)&\uliner{1}&&&\uliner{8,9}&&&\uliner{5,6}
\end{array}
\end{align*}
(2)で問われたのは下線を付した箇所のみですが，それらの“間”を補おうとしてみたくなりませんか？このとき，〔表＃〕が，上表の $k=0$ に対応するものであることに気付けば，次のようになるのではないか？と予想が立ちますね．
$\scriptsize
\begin{array}{c|c|c|c|c|c|c|c|c|c|c|c}
n&10k&10k+1&10k+2&10k+3&10k+4&10k+5&10k+6&10k+7&10k+8&10k+9\\
\hline
f(n)&3k+1&3k+1&3k+1&3k+1&3k+2&3k+2&3k+2&3k+3&3k+3&3k+3
\end{array}
$
つまり，〔表＃〕の続きは
\begin{align*}
&\begin{array}{c|c|c|c|c|c|c|c|c|c|c}
n&10&11&12&13&14&15&16&17&18&19\\
\hline
f(n)&4&4&4&4&5&5&5&6&6&6
\end{array}\\
&\begin{array}{c|c|c|c|c|c|c|c|c|c|c|c}
n&20&21&22&23&24&25&26&27&28&29\\
\hline
f(n)&7&7&7&7&8&8&8&9&9&9
\end{array}\\
&\hskip30mm
\vdots
\end{align*}
のように，
ただし，⑤の小数部分 $\beta$ は，⑤$'$ を見ればわかるように，$k\geqq10$ となると 1 を超えてしまい，「小数部分」とは呼べなくなりますから，上記(◆)のルールは崩れてしまいます．実際，$k=10$ のときを調べてみると \begin{align*} &f(100)=f(101)=f(102)=31,\ (長さ 3 の連続部分)\\ &f(103)=32 \end{align*} となっています．
さて，ルール(◆)は崩れた訳ですが，
次に，首位に関して見て行くと，〔表＃〕において，連続部分の先頭では，首位 $g(n)$ は必ず 1 になっています．このように，連続部分の中で何番目であるかによって，ある程度首位は決まってくるのではないかと考えられます．
ここまで見抜けたら，残された課題は次の2つです．
- $g(n)=4$ となる $n$ は，「長さ 3 の連続部分」や「長さ 4 の連続部分」の中の何番目か？
- 「長さ 3 の連続部分」，「長さ 4 の連続部分」がそれぞれ何回現れるか？
，
で解説します．
の 1° について．
「長さ 3 の連続部分」，「長さ 4 の連続部分」となるための，その先頭に関する条件を常用対数の小数部分に着目して表し，連続部分の各数について，常用対数の小数部分の大きさを考えれば，各々の首位を特定することができます．その結果，(3)を解くための１つの重要な鍵である(☆)が得られました．
なお，この作業過程では，$1-a=1-\log_{10}2=\log_{10}{10}-\log_{10}2=\log_{10}\bun{10}2=\log_{10}5$ などを暗算で片付けています．このくらいの計算はサラサラできないと，問題の“内容”を考える余裕など生まれません．
の 2° について．
残されたもう1つの鍵は，$0\leqq n\leqq 2018$ において，「長さ 3 の連続部分」，「長さ 4 の連続部分」がそれぞれ何回現れるかです．これを求めるには，“切りのいい所”，つまり，2018 以下の $n$ における最後の連続部分の末尾に注目します．
ここでも，(1)で求めた $\log_{10}2^{2018}$ の値①の小数部分 $0.47854$ を見れば， $\log_{10}2=0.30103$ を 2 回引けば，整数部分が減ることが読み取れます．つまり，2 つ前の「2016まで」が“切りのいい所”です．
あとは，$f(0),f(1),f(2),\cdots,f(2016)$ の「個数」と「値の種類の数」に注目して「長さ 4 の連続部分」の回数 $x$ に関する方程式⑨を立てて $x$ を求めればよいですね．
なお，上記
の(◇)，および
の部分の証明は，対数を用いずに済ますこともできます．
〔
の(◇)の証明〕
長さ 2 以下の $n$ から始まる連続部分があるとしたら，
次に，長さ 5 以上の $n$ から始まる連続部分があるとしたら，
〔
の証明〕$\circ$ 長さ 3 の連続部分 $n,n+1,n+2$ について．
$g(n)\geqq2$ だとすると，$2^{n-1}=\bun12\cdot2^n$ より，$f(n-1)=f(n)$ となり不合理だから，$g(n)=1$．
これと $2^{n+1}=2\cdot2^n$ より，$g(n+1)=2,3$．
これと $2^{n+2}=2\cdot2^{n+1}$ より，$g(n+2)=4,5,6,7$．ただし，$g(n+2)=4$ だとすると，$2^{n+3}=2\cdot2^{n+2}$ より，$f(n+3)=f(n+2)$ となり不合理．よって，$g(n+2)=5,6,7$．
$\circ$ 長さ 4 の連続部分 $n,n+1,n+2,n+3$ について．
上記と同様にして，$g(n)=1$．
よって，同様に $g(n+1)=2,3$．ただし，$g(n+1)=3$ だとすると，$2^{n+3}=4\cdot2^{n+1}$ より，$f(n+3)\gt f(n+1)$ となり不合理．よって，$g(n+1)=2$．
これと $2^{n+2}=2\cdot2^{n+1}$ より，$g(n+2)=4,5$．ただし，$g(n+2)=5$ だとすると，$2^{n+3}=2\cdot2^{n+2}$ より，$f(n+3)\gt f(n+2)$ となり不合理．よって，$g(n+2)=4$．
これと $2^{n+3}=2\cdot2^{n+2}$ より，$g(n+3)=8,9$．
上記の結果，あるいは $\smkk{解答}$ の⑦⑧をまとめると，首位は次のようになっています．
\begin{align*}
\begin{array}{c||c|c|c|c}
連続部分内での番号&1&2&3&4\\
\hline
長さ 3 の連続部分&1&2,3&5,6,7&\\
\hline
長さ 4 の連続部分&1&2&4&8,9
\end{array}
\end{align*}
なお，この表に書いたことは，厳密にいうと「必要条件」でしかありません．例えば，長さ 3 の連続部分の 2 番目の首位として，2 と 3 が両方とも現れることまでは証明してはいません．実際には，$n=5,8$ のときを考えれば，「両方とも現れる」ことも言えますが(〔表＃〕で確認できます)．他に関しても，実際に表中の全ての首位が現れます．
「$\log_{10}2$」という値は，実は無理数であり，無限小数です．入試ではよく概算値として「$0.3010$」が用いられますが，本問は，けっこう大きな $n$(2018) まで扱うので，これでは正しい結果が得られません．一番小さい所で， $n=196$ のとき早くも狂いが生じます．
そこで，本問では，より精度の高い概算値：「$0.30103$」を用いています．筆者は，さらに精度の高い概算値：「$0.301029995663981$」を用いたときと比べて，2018 以下の全ての $n$ で桁数，首位が一致していることを確認した上で出題しています．
まとめです．とにかく本問のポイントは，自然数とその常用対数の関係性を理解し，常用対数の値そのものをよく見てそこから情報を引き出すことに尽きます．もう一度言います．求める桁数とかをすぐに「〇〇とおく」とやる人は，一生，「対数」を理解できないまま終わります．そして，ここで述べたことは，「数学」という学問全体を通して言えることでもあります．
$\smkk{参考}$
数列(数学B)，および極限(数学Ⅲ)に“習熟”した人向けのややハイレベルな参考です．
$n=0,1,2,\cdots,N$ の中で， $g(n)=4$ となる $n$ の占める割合は，$N\to\infty$ のときどんな値に近づいていくかを調べてみます．
$N\ (本問でいう 2018)$ 番以下で，最後の連続部分の末尾(本問でいう 2016)を $M$ とすると，
\begin{align*}
M=N-r\ (r=0\ \mr{or}\ 1\ \mr{or}\ 2\ \mr{or}\ 3)
\end{align*}
と表せる．
\begin{align*}
f(0)=1,f(1),f(2),\cdots,f(M)：\lbrc{
個数：M+1 個\\
値：f(M) 種類
}
\end{align*}
について考える．
\begin{align*}
f(M) 種類の値\lbrc{
長さ 4 の連続部分\cdots x 種類\\
長さ 3 の連続部分\cdots f(M)-x 種類
}
\end{align*}
とすると
\begin{align*}
4x+3\brc{f(M)-x}=M+1.\quad \thr\ x=M+1-3f(M).
\end{align*}
$g(n)=4$ となる $n$ の個数は $x$ であり，これが $n=0,1,2,\cdots,N$ の中に占める割合は
\begin{align*}
\bun x{N+1}=&\bun{M+1-3f(M)}{N+1}\\
=&\bun{M+1-3f(M)}M\cdot \bun M{N+1}\\
=&\prn{1+\bun1M-3\cdot \bun{f(M)}M}\cdot \bun M{N+1}.
\end{align*}
ここで，$N\to\infty$ のときを考える．このとき，$M\to\infty$ であり， $\log_{10}2^M$ の整数部分は $f(M)-1$ だから
\begin{align*}
&f(M)-1\leqq\log_{10}2^M\lt f(M).\\
&Ma\lt f(M)\leqq Ma+1.\ \prn{a=\log_{10}2}\\
&a\lt \bun{f(M)}M\leqq a+\bun1M\to a.
\end{align*}
よって，はさみうちにより $\bun{f(M)}M\to a$ ．
また，
\begin{align*}
\bun M{N+1}=&\bun{N-r}{N+1}\\
=&\bun1{1+\frac1N}-\bun{r}{N+1}\to1.
\end{align*}
以上より
\begin{align*}
\bun x{N+1}\to1-3a=1-3\log_{10}2.
\end{align*}
これは，$1-3\cdot 0.3=0.1$ より少しだけ小さい値ですから，「首位 4」の出現率は，$\bun1{10}$ 弱ということになります．(3)の答え：196 も，$0,1,2,\cdots,2018$ の個数 2019 の $\bun1{10}$ 弱になっていますね．
ちなみに，解説の表をもとに上記と同様に考えると，首位における 1～9 の各数の出現率の極限は，次のようになることがわかります．
\begin{align*}
\begin{array}{c|c|c|c|c|c}
首位&1&2,3&4&5,6,7&8,9\\
\hline
出現率&a&a&1-3a&4a-1&1-3a\\
\hline
概算値&0.3&0.3&0.1&0.2&0.1
\end{array}
\end{align*}
首位としては，「1」が断然現れやすいことがわかりますね．
