第4弾 解答・解説
$f(\theta)$ の最大値 $M$ は， $f(\theta)$ がこのままの形では求まりそうにないですね．では，どのように変形したらよいでしょう？
「このまま」では上手く行かない理由は，変数 $\theta$ が 3 か所にあって各部がそれぞれ変化し，$f(\theta)$ 全体の変化がよくわからないことです．そこで，変数 $\theta$ を集めることはできないか？という発想が浮かんできます．
$\mathbf{【解答】}$
\begin{align*} f(\theta)=&\sin\theta+2\sin(\theta+\alpha)+3\sin(\theta+2\alpha)\ \cdots①\\ =&\sin\theta+2(\sin\theta\cos\alpha+\cos\theta\sin\alpha)+3(\sin\theta\cos2\alpha+\cos\theta\sin2\alpha)\ \cdots②\\ =&\underbrace{(1+2\cos\alpha+3\cos2\alpha)}_{Aとおく}\sin\theta+\underbrace{(2\sin\alpha+3\sin2\alpha)}_{Bとおく}\cos\theta\ \cdots③\\ =&\sqrt{A^2+B^2}\sin(\theta+\theta_0)\ (\theta_0 はある定角).\ \cdots④ \end{align*} よって $f(\theta)$ の最大値 $M$ は \begin{align*} M=&\sqrt{A^2+B^2}. \end{align*} 以下，$M$ の最小値を考える． \begin{align*} M^2=&A^2+B^2\\ =&(1+2\cos\alpha+3\cos2\alpha)^2+(2\sin\alpha+3\sin2\alpha)^2\ \cdots⑤\\ =&14+2(2\cos\alpha+3\cos2\alpha+6\cos\alpha)\ \cdots⑥\\ =&14+2(3\cos2\alpha+8\cos\alpha)\ \cdots⑥’\\ =&14+2\cdot\underbrace{\{3(2\cos^2\alpha-1)+8\cos\alpha\}}_{Fとおく}.\ \cdots⑦ \end{align*}
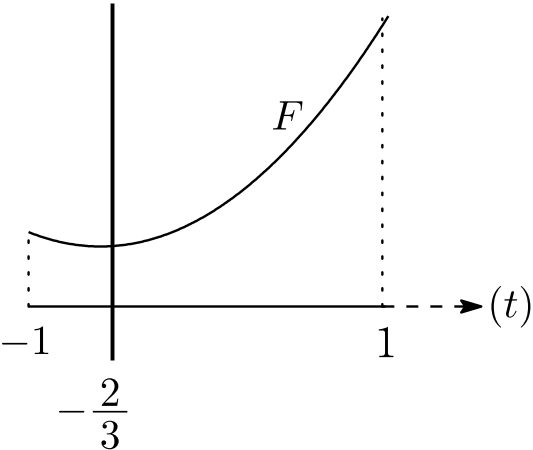ここで， $t=\cos\alpha$ とおくと， $t$ の変域は $0\leqq\alpha\leqq\pi$ より $-1\leqq t\leqq1$ であり，
\begin{align*}
F=&6t^2+8t-3\ \cdots⑧\\
=&6\begin{pmatrix}t+\displaystyle \frac23\end{pmatrix}^2-\displaystyle \frac{17}3.
\end{align*}
よって $F$ は $t=-\displaystyle \frac23$ のとき最小となり，$M\geqq0$ だから，$M$ もこのとき最小となる．このときの $\alpha=\alpha_1$ は，次を満たす．
\begin{align*}
\cos\alpha_1=\displaystyle \frac{\boxed{-2}^{アイ}}{\boxed{3}_{ウ}}.
\end{align*}
また， $0\leqq\alpha_1\leqq\pi$ より
\begin{align*}
\sin\alpha_1=&\sqrt{1-\begin{pmatrix}-\displaystyle \frac23\end{pmatrix}^2}=\displaystyle \frac{\sqrt{\boxed{5}}^{エ}}{\boxed{3}_{オ}}.
\end{align*}
さらに，$F$ の最小値は $-\displaystyle \frac{17}3$．よって $M^2$ の最小値は⑦より
\begin{align*}
14+2\begin{pmatrix}-\displaystyle \frac{17}3\end{pmatrix}=&\displaystyle \frac83.
\end{align*}
よって $M$ の最小値は， $\displaystyle \frac{2\sqrt2}{\sqrt3}=\displaystyle \frac{^{カ}\boxed{2}\sqrt{\boxed{6}}^{キ}}{\boxed{3}_{ク}}$ ．$\mathbf{【解説】}$
まずは一般論から．三角関数に限らず，関数全般に関して，基本となる変形方針を確認しておきましょう．次のような目的をもって行うと上手くいくことが多いです．
- 変数を１か所に集める．
$\mathbf{[例]}$： $x^2-6x=(x-3)^2-9$．( 2次関数を平方完成して $x$ を集める．) - 関数の種類を統一する．
$\mathbf{[例]}$：$\log_2x+\log_4x=\log_2x+\displaystyle \frac{\log_2x}{\log_24}$ ( 対数の底を統一する．) - 次数を変える
$\mathbf{[例]}$： $\cos^2\theta=\displaystyle \frac{1+\cos2\theta}2$．( 「半角公式」により，「2次」から「1次」へと次数下げ．)
～
で，①式から④式へ，および⑤式から⑦への変形に関して，その目的と方法を解説していきます．
①→② の変形
本問の $f(\theta)$ は3つの三角関数 $\sin\theta$ ， $\sin(\theta+\alpha)$ ，$\sin(\theta+2\alpha)$ で構成されています．3つとも「 $\sin$ 」ですから，ある意味では“種類”はそろっているとも言えますが，それぞれの角が $\theta\ ,\theta+\alpha\ ,\theta+2\alpha$ と全て異なっているので困ります．そこで， (b) に基づき，$\sin(\theta+\alpha)$ ，$\sin(\theta+2\alpha)$ に「加法定理」を適用して，角を $\theta$ に統一します．
②→③ の変形
関数 $f(\theta)$ の最大値 $M$ を求める際には，$\theta$ が変数， $\alpha$ は定数と考えます．よって②を整理するには，「 $\sin\theta$ の係数，$\cos\theta$ の係数はそれぞれ何か？」と考え，③のようにまとめます．
③→④ の変形
$\alpha$ で表された前記2つの「係数」は，あくまでも「定数」にすぎません．ただ，ちょっと長い式なので「 $A$ 」，「 $B$ 」と簡潔な“名前”を与えて「 $A\sin\theta+B\cos\theta$ 」と表します．これは，「合成公式」によって変数 $\theta$ を1か所に集めることができる形ですね！「合成」することの狙い，それは (a) そのものです．
それでは「合成公式」の使い方を確認しておきましょう． $f(\theta)$ を合成するときの考え方は，次の通りです．
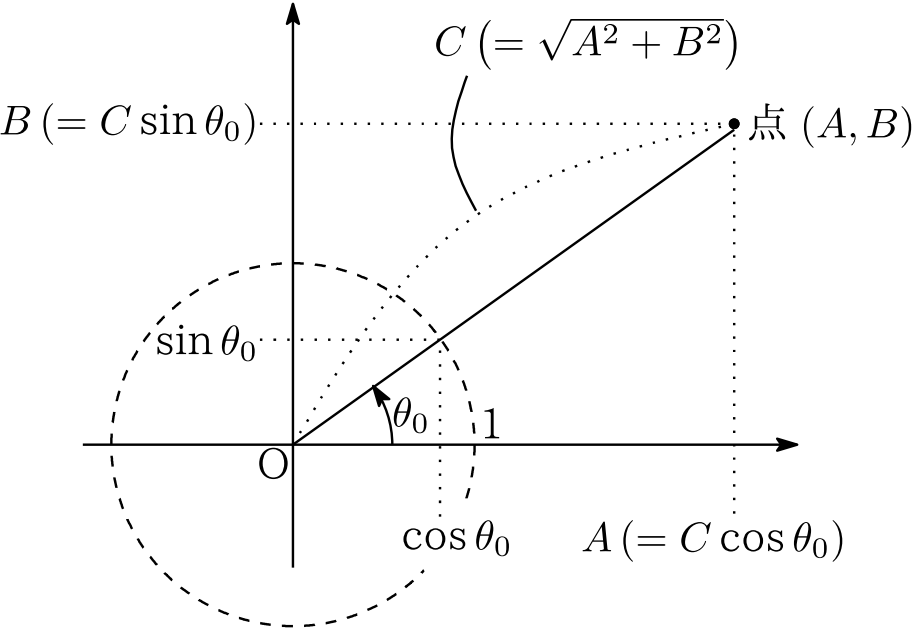
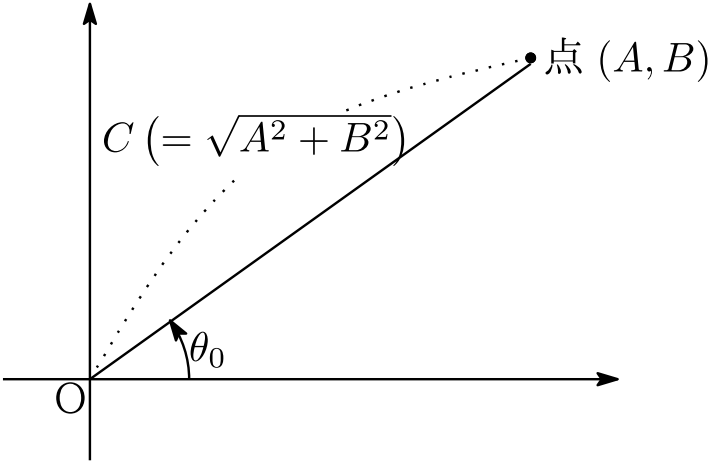
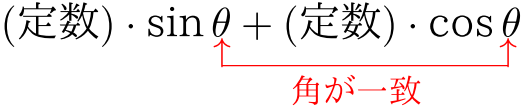
- $f(\theta)=A\sin\color{red}{\underline{\color{black}{\theta}}}+B\cos\color{red}{\underline{\color{black}{\theta}}}\ (A\ ,Bは定数)$ において，2つの角が一致していることを確認する．このようなときは $C\sin(\theta+\theta_0)\ (C\ ,\theta_0 は定数)$ の形へと「合成」できることを覚えておく．
- 前記 $C\ ,\theta_0$ を求める．加法定理を用いると
\begin{align*}
C\sin(\theta+\theta_0)=&\color{red}{\underline{\color{black}{C\cos\theta_0}}}\cdot\sin\theta+\color{red}{\underline{\underline{\color{black}{C\sin\theta_0}}}}\cdot\cos\theta.\
\end{align*}
これと
\begin{align*}
f(\theta)=\color{red}{\underline{\color{black}{A}}}\sin\theta+\color{red}{\underline{\underline{\color{black}{B}}}}\cdot\cos\theta
\end{align*}
とで， $\color{red}{\underline{\color{black}{\sin\theta\ の係数}}}$ ，$\color{red}{\underline{\underline{\color{black}{\cos\theta\ の係数}}}}$どうしを比較すると
\begin{eqnarray}
\left\{
\begin{array}{l}
C\cos\theta_0=A\ ,\\\
C\sin\theta_0=B\ .\
\end{array}
\right.
\end{eqnarray}
これは，右図のように $C\ ,\theta_0$ をとれば成り立つ．(半径が1である単位円周上の点の座標をもとに考えれば納得できますね．)
- よって
\begin{align*}
f(\theta)=\sqrt{A^2+B^2}\sin(\theta+\theta_0)\ (\theta_0 は図の定角)
\end{align*}
と合成できた．
なお，図の角 $\theta_0$ は，点 $(A,B)$ の「偏角」といわれるものです．「偏角」という単語は，高校教科書では数学Ⅲで登場します．
それから，ここでいう「定角」とは，詳しくいうと「変数 $\theta$ によらない角」という意味です．
以上の考え方を理解した上で，実際に合成するときは，次のようにササっと済ませます．- 座標平面上に， $f(\theta)$ の $\sin\theta$ の係数，$\cos\theta$ の係数をそれぞれ横座標，縦座標とする点 $(A\ ,\ B)$ をとる．
- 点 $(A\ ,\ B)$ の原点からの距離，偏角を用いて \begin{align*} A\sin\theta+B\cos\theta=\sqrt{A^2+B^2}\sin(\theta+\theta_0)\ \cdots⑨ \end{align*} とする．(以上！)
$\mathbf{＜参考＞}$ここまでは， $(A\ ,\ B)\ne(0\ ,\ 0)$ を前提とし，ちゃんと点 $(A\ ,\ B)$ の偏角が定まる状況で考えました． では，$(A\ ,\ B)=(0\ ,\ 0)$ のときはというと・・・⑨式は両辺がともに「0」ですからちゃんと成り立ちます．つまり，$(A\ ,\ B)=(0\ ,\ 0)$ のときでも「合成」はできるんです．ただし， 「$\theta_0$」 の所はどんな定数でもOKなので，定まりはしませんが．
前記 $\mathbf{【解答】}$ では，万が一「$(A\ ,\ B)=(0\ ,\ 0)$ 」のケースがあったとしても大丈夫なように，「 $\theta_0$ は
④において， $\sin(\theta+\theta_0)$ は $-1$ ～ $1$ の任意の値をとりますから， $f(\theta)$ の最大値は $M=\sqrt{A^2+B^2}$ だとわかりました．そこで以下，⑤式から⑦式への変形を解説します．
⑤→⑥ の変形
⑤を展開すると，次のようになります．
\begin{align*}
&(1+2\cos\alpha+3\cos2\alpha)^2+(2\sin\alpha+3\sin2\alpha)^2\ \cdots⑤\\
=&1+4\cos^2\alpha+9\cos^22\alpha+4\cos\alpha+6\cos2\alpha+12\cos\alpha\cos2\alpha\\
&\hskip0.5em+4\sin^2\alpha+9\sin^22\alpha\hskip8.8em+12\sin\alpha\sin2\alpha\ \cdots⑤’\\
=&1+4\hskip2.8em+9\hskip3.2em+4\cos\alpha+6\cos2\alpha+12(\cos\alpha\cos2\alpha+\sin\alpha\sin2\alpha)\ \cdots⑤’’\\
=&14+4\cos\alpha+6\cos2\alpha+12\cos(2\alpha-\alpha).
\end{align*}
これで(ほぼ)⑥が得られました．ただし，⑤$'$ は実際には紙に書かず，縦にそろっている項どうしの和を，たとえば 「$4\cos^2\alpha+4\sin^2\alpha=4$ 」のように暗算で済ませてから紙に書くよう訓練しましょう．このように，ある程度先を見通しながら計算する習慣をつけると，様々な局面で正しい方針が選択できるようになるんです．
⑤$''$ の括弧内は， $\cos$ の加法定理の右辺の形ですね．できればこれも紙に書かず，⑤を見ながら「 $\cos\alpha\cos2\alpha$ と $\sin\alpha\sin2\alpha$ を合わせると加法定理で $\cos(2\alpha-\alpha)$ つまり $\cos\alpha$ になるな」と，暗算で片づけるのが理想です．
「とても無理っ！！」って思う人もいるでしょうが，訓練すると結構できるんですよこれが．(実際，筆者が指導している高2の生徒さんは，かなりできます．普段から鍛えてますんで！)
⑥→⑦ の変形
⑥には $\cos\alpha$ と $\cos\color{red}{\underline{\color{black}{2}}}\alpha$ が混在しています．そこで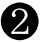， に続いて再び (b) に基づいて角を $\alpha$ に統一します．
$\cos$ の2倍角公式には
\begin{eqnarray}
\cos2\alpha=
\begin{cases}
\cos^2\alpha-\sin^2\alpha\ ,\\\
2\cos^2\alpha-1\ ,\\\
1-2\sin^2\alpha
\end{cases}
\end{eqnarray}
と3通りの形がありますが，「 $\cos\alpha$ 」に統一したいのですから，当然2番目の形を用います．
以上で，三角関数を加法定理などによって変形する作業は終了です．(お疲れ様でした・・・)
$M^2$ が $\cos\alpha$ だけで表せたので， $t=\cos\alpha$ と置換し， $t$ の2次関数の最小値を考えることに帰着させます．その際には，置換して得られた変数 $t$ の変域に注意し，「定義域」と「軸」の位置関係に注目します．
ちなみに， $M$ が最小になるときの $\alpha=\alpha_1$ の大きさは， $\cos\alpha_1=\displaystyle \frac{-2}3$ より，おおよそ $2.3$ [rad] (度数法で約132°)です．
以上を振り返ってみて，本問でもっとも重要な役割を演じた公式は，やはり ：「③から④への変形」で用いた「合成公式」でしょう．そこで，そもそもどんなときに合成することができるのかを確認しておきましょう．
結論はごく単純です．
$\cdots$ ⑩
で述べた方法により，1つの $\sin$ に合成できます．次に，
\begin{align*}
\sin(\theta+\beta)\ ,\sin(-\theta+\beta)\ ,\cos(\theta+\beta)\ ,\cos(-\theta+\beta)\ \cdots⑪
\end{align*}
のような $\theta$ の係数が $1$ or $-1$ である三角関数 $\sin\ ,\cos$ ，つまり周期が $2\pi$ である $\sin\ ,\cos$ の各々は，本問の $\mathbf{【解答】}$ と同じように加法定理を適用すれば，角が統一された⑩式の形になります．よって⑪のような関数の定数倍の和も，全体が⑩の形になり，合成公式により「1つの $\sin$ 」にまとまる訳です．実際，本問の関数 $y=f(\theta)$ のグラフは，次図のようなきれいなサインカーブとなります．(これは， $\alpha=\alpha_1$ のときのグラフです．)
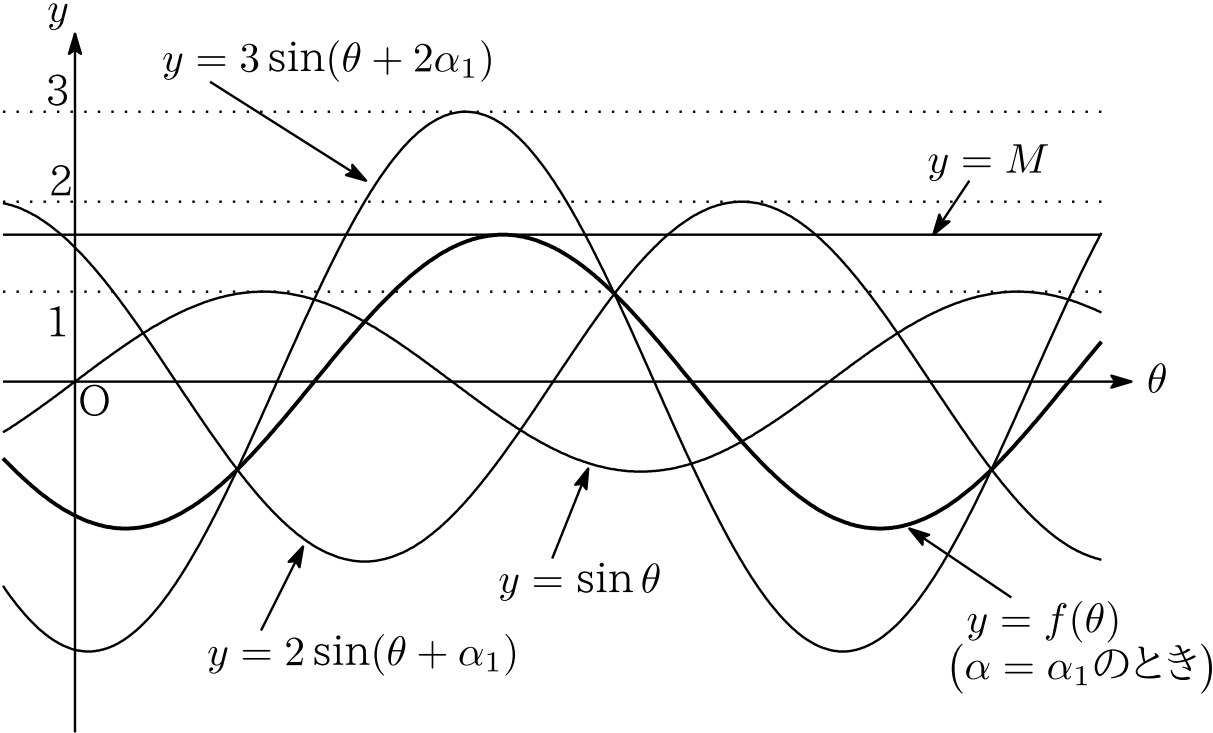
では，周期の異なる三角関数の和だとどうなるでしょう．たとえば関数
\begin{align*}
g(\theta)=2\sin\theta+\sin\color{red}{\underline{\color{black}{2}}}\theta
\end{align*}
において， $\sin\theta $ と $\sin\color{red}{\underline{\color{black}{2}}}\theta$ の周期は異なり，グラフを描いてみると次のようになります．
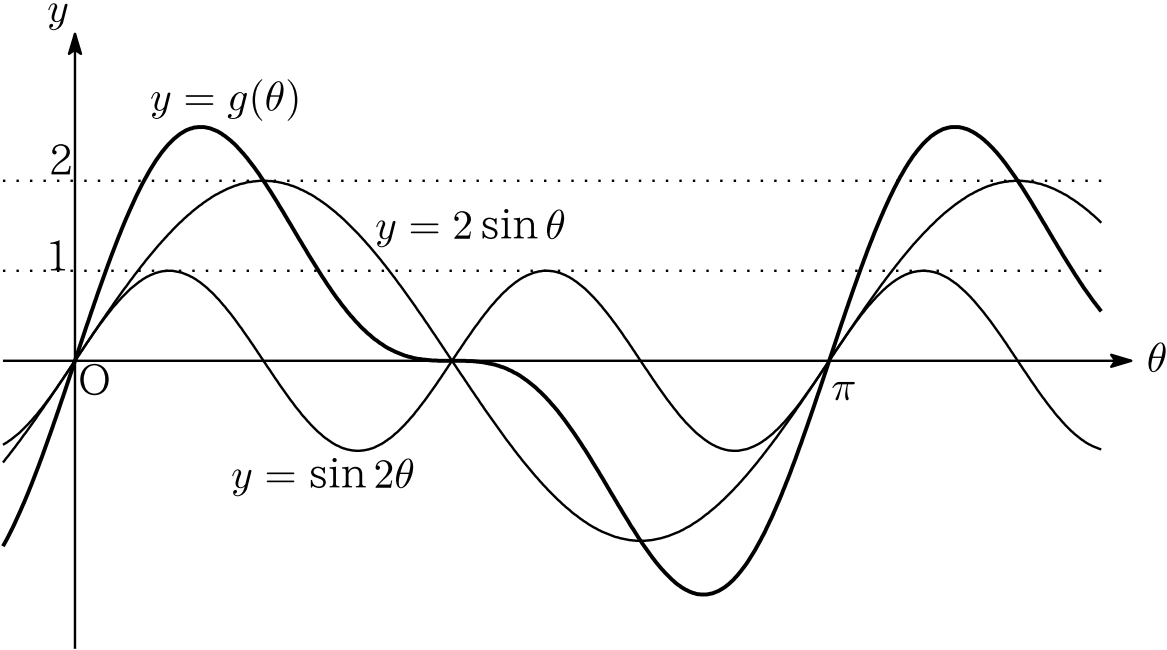
$\mathbf{【解答】}$ ⑥$'$ 式の括弧内： $3\cos\color{red}{\underline{\color{black}{2}}}\alpha+8\cos\alpha$ を $\alpha$ の関数とみた場合にも同じことが言えます．1つの $\sin$ にまとめる，つまり $\alpha$ を集めることができない．そこで，
の基本変形方針のうち，(b)：「 $\cos\alpha$ に統一」を使いました．
$M$ が最大となるのは，$\mathbf{【解答】}$ にある2次関数のグラフからわかるように，$t=1$ のときです．このとき
\begin{align*}
F=6\cdot 1^2+8\cdot1-3=11
\end{align*}
で，これと⑦より $M$ の最大値は
\begin{align*}
\sqrt{14+2\cdot 11}=6
\end{align*}
となります．
$t=1$ のときに $M$ が最大となることは，次のように直感的に納得することもできます．$t=\cos\alpha=1$ のとき， $\alpha=0$ より
\begin{align*}
f(\theta)=\sin\theta+2\sin\theta+3\sin\theta(=6\sin\theta)
\end{align*}
となります．3つある $\sin$ は，角が完全に一致しているので，全て同時に最大となります．よって，これらの和である $f(\theta)$ の最大値がもっとも大きくなるのです．一方，解説 のグラフのように， $f(\theta)$ を構成する3つの $\sin$ が最大となるタイミングがズレていると， $f(\theta)$ の最大値はあまり大きくなれない訳です．
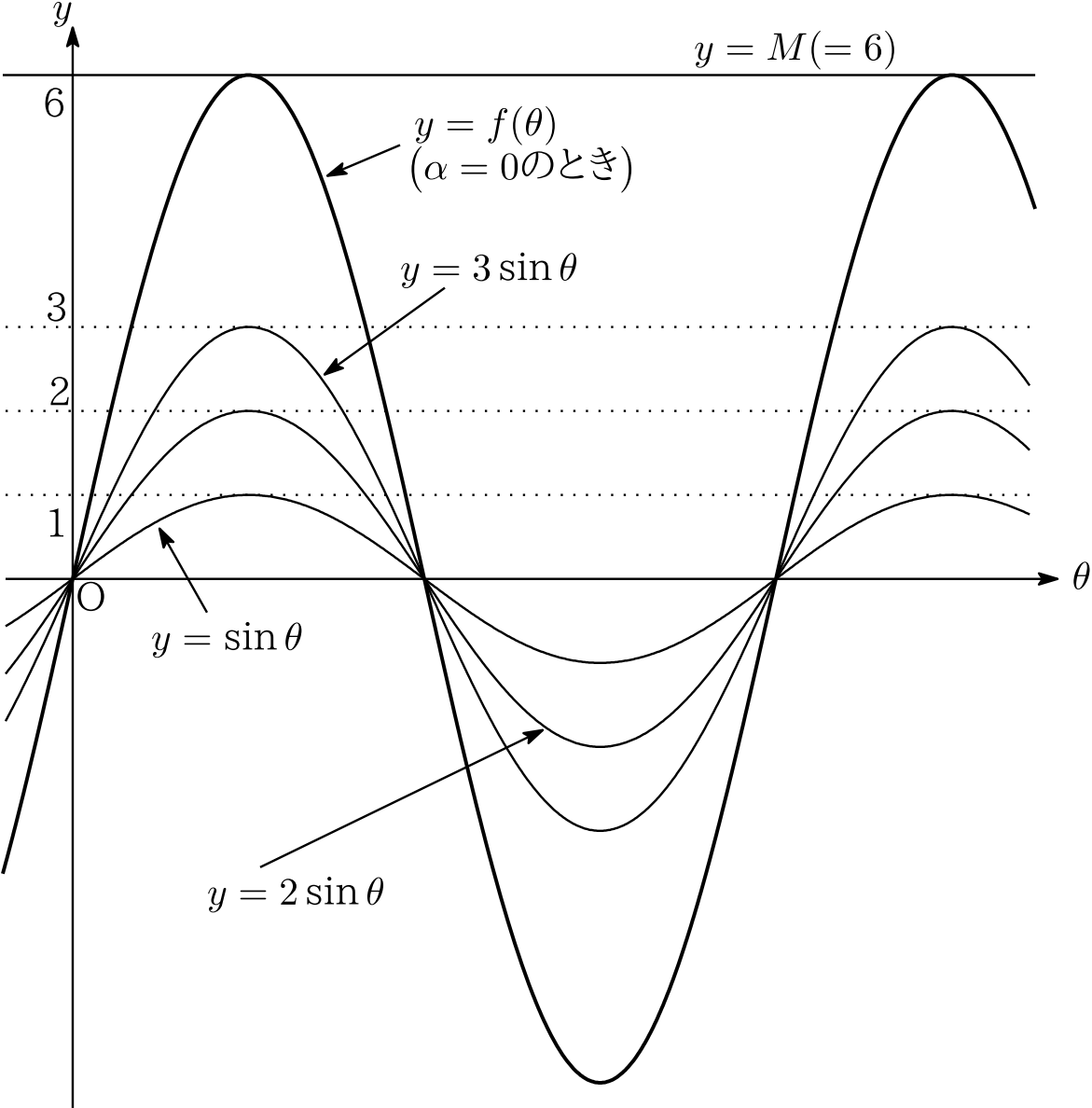
本問を少し変えて， $\theta$ の関数
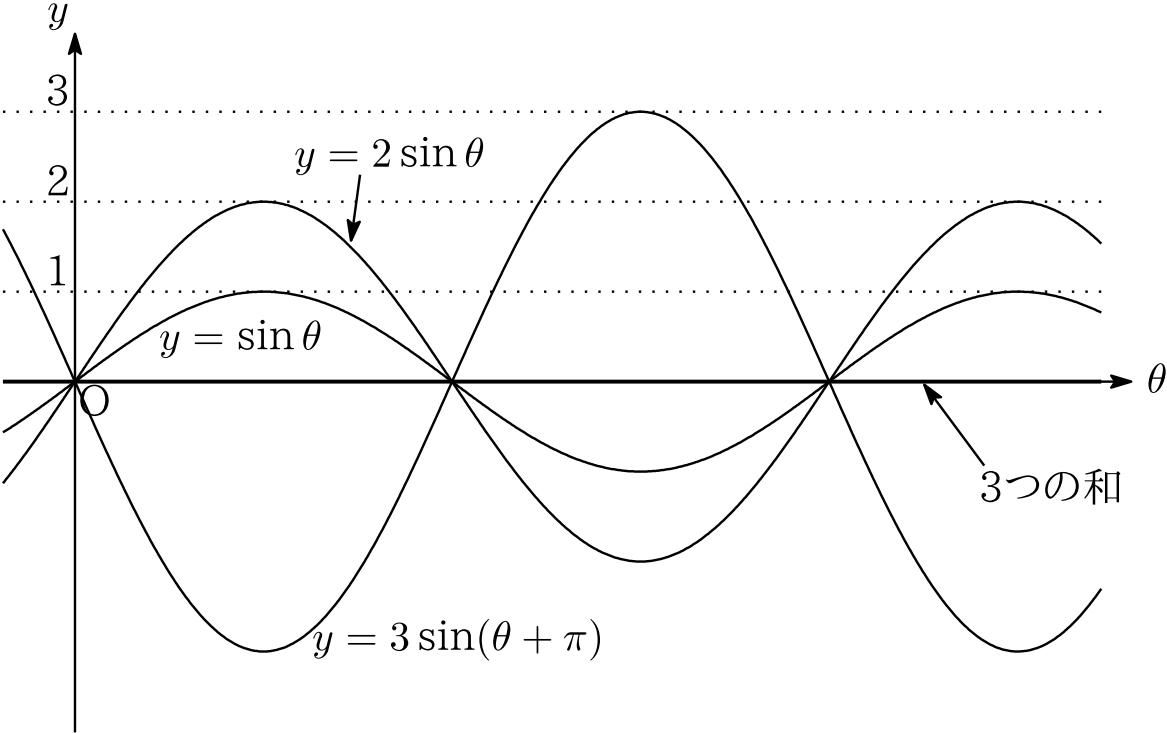
\begin{align*}
h(\theta)=&\sin\theta+2\sin(\theta+\alpha)+3\sin(\theta+\color{red}{\color{red}{\underline{\color{black}{\beta}}}})
\end{align*}
を考えてみましょう． 「 $\beta$ 」は，「 $2\alpha$ 」と違って $\alpha$ とは無関係に値をとることができますから
\begin{align*}
\alpha=0\ ,\ \beta=\pi
\end{align*}
とできます．このとき
\begin{align*}
h(\theta)=&\sin\theta+2\sin\theta+3\sin(\theta+\pi)\\
=&\sin\theta+2\sin\theta-3\sin\theta=0
\end{align*}
となり， $h(\theta)$ の値はつねに 0 です．(つまり， $h(\theta)$ の最大値も「 0 」ですね．)
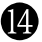これ以降は，「ベクトル」(数学Ｂ)にも習熟している人向けの，ややハイレベルな内容です．
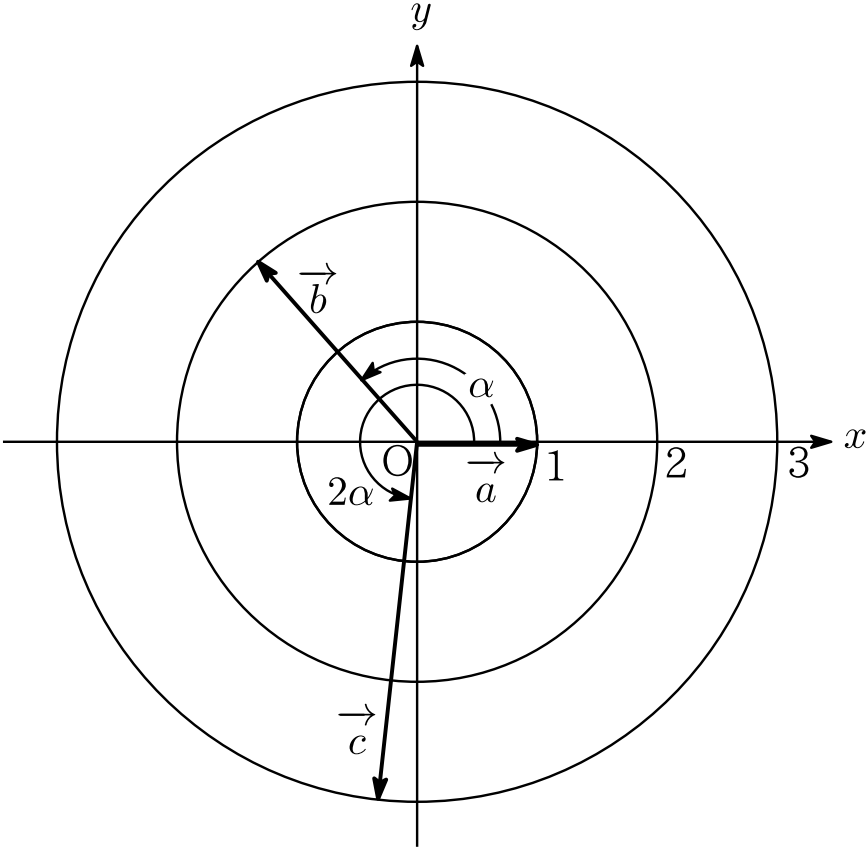
$\mathbf{【解答】}$の $M=\sqrt{A^2+B^2}$ はベクトル
\begin{align*}
\overrightarrow{u}=&\begin{pmatrix}1+2\cos\alpha+3\cos2\alpha\\\phantom{0+\,}2\sin\alpha+3\sin2\alpha\end{pmatrix}\\
=&\begin{pmatrix}1\\0\end{pmatrix}+2\begin{pmatrix}\cos\alpha\\\sin\alpha\end{pmatrix}+3\begin{pmatrix}\cos2\alpha\\\sin2\alpha\end{pmatrix}
\end{align*}
の 大きさ $\left|\overrightarrow u\right|$ に他なりません．そこで， $\overrightarrow a=\begin{pmatrix}1\\0\end{pmatrix},\overrightarrow b=\begin{pmatrix}\cos\alpha\\\sin\alpha\end{pmatrix},\overrightarrow c=\begin{pmatrix}\cos2\alpha\\\sin2\alpha\end{pmatrix}$ とおき，内積の演算法則を用いて， $\left|\overrightarrow u\right|^2$ を計算してみましょう．
\begin{align*}
&\left|\overrightarrow a\right|=\left|\overrightarrow b\right|=\left|\overrightarrow c\right|=1\ ,\\
&\overrightarrow a\cdot\overrightarrow b=\cos\alpha\ ,\ \overrightarrow a\cdot\overrightarrow c=\cos2\alpha\ ,\\
&\overrightarrow b\cdot\overrightarrow c=\cos2\alpha\cos\alpha+\sin2\alpha\sin\alpha=\cos(2\alpha-\alpha)=\cos\alpha.
\end{align*}
これらを用いると
\begin{align*}
\left|\overrightarrow u\right|^2=&\left|\overrightarrow a+2\overrightarrow b+3\overrightarrow c\right|^2\\
=&(\overrightarrow a+2\overrightarrow b+3\overrightarrow c)\cdot(\overrightarrow a+2\overrightarrow b+3\overrightarrow c)\\
=&\left|\overrightarrow a\right|^2+4\left|\overrightarrow b\right|^2+9\left|\overrightarrow c\right|^2+4\overrightarrow a\cdot\overrightarrow b+6\overrightarrow a\cdot\overrightarrow c+12\overrightarrow b\cdot\overrightarrow c\\
=&1+4+9+4\cos\alpha+6\cos2\alpha+12\cos\alpha\\
=&14+6\cos2\alpha+16\cos\alpha
\end{align*}
これは，⑥’式とたしかに一致していますね．
じつは，本問で扱った関数 $f(\theta)$ 自体が，ベクトル
\begin{align*}
\overrightarrow{v}=\begin{pmatrix}\cos\theta\\\sin\theta\end{pmatrix}+2\begin{pmatrix}\cos(\theta+\alpha)\\\sin(\theta+\alpha)\end{pmatrix}+3\begin{pmatrix}\cos(\theta+2\alpha)\\\sin(\theta+2\alpha)\end{pmatrix}
\end{align*}
の $y$ 成分です．
$\overrightarrow p=\begin{pmatrix}\cos\theta\\\sin\theta\end{pmatrix},$$\overrightarrow q=2\begin{pmatrix}\cos(\theta+\alpha)\\\sin(\theta+\alpha)\end{pmatrix},$$\overrightarrow r=3\begin{pmatrix}\cos(\theta+2\alpha)\\\sin(\theta+2\alpha)\end{pmatrix}$ とおきましょう．$\theta$ が増加するとき，これら3つのベクトルは同じ角ずつ回転するので相互の位置関係は不変です．よって $\overrightarrow v$ は，大きさを一定に保ちながら回転していきますから，その $y$ 成分である $f(\theta)$ の最大値 $M$ とは， ベクトル $\overrightarrow v$ の大きさ $\left|\overrightarrow v\right|$ そのものです．そして，その大きさは $\theta$ の値によらず一定なので，簡単のため $\theta=0$ のときの $\overrightarrow v$ を考えればよく，それは前述のベクトル $\overrightarrow u$ と一致していますね．
おおまかなイメージとしては，3ベクトル $\overrightarrow p\ ,\overrightarrow q\ ,\overrightarrow r$ が互いに“打ち消し合って”大きさが小さくなるような相互関係になっているときに， $M$ は最小となる訳です．
