第5弾 解答・解説
本問で問われている内容は，(1)～(4)まで終始一貫して，点Pが
$\mathbf{【解答】}$
(1) $X:5→0$ と移動するのは，5 の目が出るときだから，この確率は，
$
\dfrac{\boxed1^{ア}}{\boxed6^{イ}}.
$
$X:-2→0$ 以外へ移動するのは，2 以外の目が出るときだから，この確率は，
$
\dfrac{\boxed5^{ウ}}{\boxed6^{エ}}.
$
(2)
各回における2つの状態 $O,A$ を
\begin{eqnarray}
\left\{
\begin{array}{l}
O:X=0,\\
A:X=\pm1,\pm2,\pm3,\pm4,\pm5,6
\end{array}
\right.
\end{eqnarray}
よって求める確率は \begin{align*} &(n-3)\times1\cdot\dfrac16\cdot1\cdot\left(\dfrac56\right)^{n-4}\cdot\dfrac16\ \cdots②\\ =&\dfrac{n-\boxed3^{ケ}}{\boxed{36}_{コサ}}\cdot\left(\dfrac{\boxed5^{シ}}{\boxed6^{ス}}\right)^{n-\boxed{\scriptsize 4}^{\small セ}}. \end{align*} (4) 2つの事象 $E,F$ を次のように定める． \begin{align*} E:&「n 回後に\mathrm Pが\mathrm Oにあり，途中で2回だけ\mathrm Pが\mathrm Oに戻る」\\ F:&「3回後に\mathrm Pが原点\mathrm Oにある」 \end{align*} 求める条件付き確率は \begin{align*} P_E(F)=\dfrac{P(E\cap F)}{P(E)}.\ \cdots③ \end{align*} $E$ は，次のような事象である． \begin{align*} ^{\raise{0.5em}{回}}_{\lower{1.0em}{確率}}O\xrightarrow[1]{1}A\underbrace{\boxed{→\cdots →}}_{n-2回の移動}A\xrightarrow[\frac16]{n}O\ \cdots④ \end{align*} ただし，上記「 $n-2$ 回の移動」の内訳は，次のようになる． \begin{eqnarray} \left\{ \begin{array}{l} A→O→A\ \cdots\ 2セット\\ \hskip2.3em A→A\ \cdots\ n-6 回\\ \end{array} \right. 計\ n-4\ 個\ \cdots⑤ \end{eqnarray} 「$A→O→A$」と「$A→A$」の並べ方は \begin{align*} {}_{n-4} \mathrm{ C }_2 通り．\ \cdots⑥ \end{align*} $E\cap F$ は，次のような事象である． \begin{align*} ^{\raise{0.5em}{回}}_{\lower{1.0em}{確率}}O\xrightarrow[1]{1}A\xrightarrow[\frac56]{2}A\xrightarrow[\frac16]{3}O\xrightarrow[1]{4}A\underbrace{\boxed{→\cdots →}}_{n-5回の移動}A\xrightarrow[\frac16]{n}O \end{align*} 上記「 $n-5$ 回の移動」の内訳は，次のようになる． \begin{eqnarray} \left\{ \begin{array}{l} A→O→A\ \cdots\ 1セット\\ \hskip2.3em A→A\ \cdots\ n-7 回\\ \end{array} \right. 計\ n-6\ 個 \end{eqnarray} 「$A→O→A$」と「$A→A$」の並べ方は \begin{align*} n-6 通り．\ \cdots⑦ \end{align*} ⑥の ${}_{n-4} \mathrm{ C }_2$ 通りの各々，および⑦の $n-6$ 通りの各々の確率は全て等しく，これを $p$ とおくと，求める条件付き確率は，③より \begin{align*} P_E(F)=&\dfrac{(n-6)\cdot p}{{}_{n-4} \mathrm{ C }_2\cdot p}\ \cdots⑧\\ =&\dfrac{2(n-\boxed6^{ソ})}{(n-\boxed4^{タ})(n-\boxed5^{チ})}. \end{align*}
$\mathbf{【解説】}$
(1)と同じように考えると，$X=\pm1,\pm2,\pm3,\pm4,\pm5,6$ のとき，$X=0$ へと移動するのはサイコロの目が次のようになるときです．
\begin{eqnarray}
\left\{
\begin{array}{l}
X=\pm 1\ →\ 1の目\\
X=\pm 2\ →\ 2の目\\
X=\pm 3\ →\ 3の目\\
X=\pm 4\ →\ 4の目\\
X=\pm 5\ →\ 5の目\\
X=\phantom{\pm}6\ →\ 6の目
\end{array}
\right.
\end{eqnarray}
このように，$X=-5,-4,-3,-2,-1,1,2,3,4,5,6$ という11個の状態は，点Pの位置としては異なるものの，原点Oへと移動する確率に関しては全て等しく $\dfrac16$ ですね．そこで，これら11個を「1つの状態$A$」 としてまとめ，
\begin{eqnarray}
\left\{
\begin{array}{l}
O:X=0,\\
A:X=\pm1,\pm2,\pm3,\pm4,\pm5,6
\end{array}
\right.
\end{eqnarray}
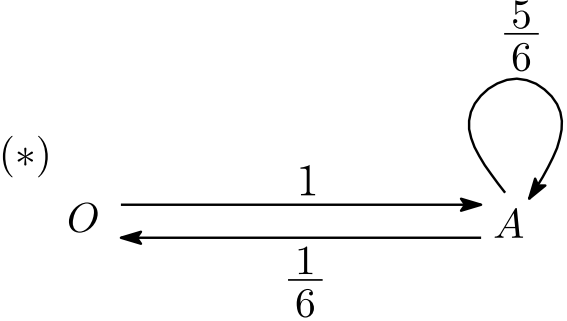
という2つだけに分類してみます．すると，この2つの状態間の推移は，(2)の図 $(\ast)$ に示した確率で起こります．じつにシンプルですね．(こんな風に複数の状態を1つにまとめて考えることを，筆者個人は普段，「束ねる」と呼んでいます．)
なお，「$X=-6$」を状態 $A$ に 含めても(2) $(\ast)$ の推移確率は変わりませんが，実際には，本問のルールに従うと「$X=-6$」となることはないことがわかります．
確率を求める際には，「$O$」や「$A$」という「各回における状態」ではなく，「$A→A$，$A→O$」などの「移動の仕方」について考えることが重要です．そして，このような移動・推移を，$\mathbf{【解答】}$ にあるように視覚的に表現し，(状態「$A,O$」ではなく)推移を表す「→」の個数を考えましょう．
なお，(2)～(4)においては，状態 $O$ の後は必ず状態 $A$ となることに注意してください．
(2)では推移の仕方が1つしかないので，単純に各推移の確率を掛け合わせれば答えが得られるのに対し，(3)では推移の順序が何通りあるかを①のように考え，その「順序の個数」を「各々の推移の確率」に掛けて②のように求めます．((4)も同様です．
)
(4)で問われた「・・・であるとき～～である条件付き確率」を求める際には，次の手順を踏みます．
1° 2つの事象「・・・である」，「～～である」に名前を付ける．($\mathbf{【解答】}$の $E,F$ )
2° 条件付き確率の定義式③を予め書いておく．
3° ③式の分母，分子をそれぞれ求める．
定義式③が示す通り，条件付き確率 $P_E(F)$ とは，事象 $E$ の起きたという前提のもとで，事象 $F$ も起きる確率，つまり，「$E$ を新たに全体とみて，それに対する $E\cap F$ の起こりやすさの割合」です．
本問(4)では，前提の $E$ が 「$n$ 回まで」のことを指し，$F$ が「3回後」のことを述べています．時間的に「後」のことを前提として「前」のことの確率を問う形になっているので「考えにくいな～」と感じるかもしれません．しかし，条件付き確率の定義式③の中には「時の流れ」だの「因果関係」だのは一切現れていませんね．ただ単に，③の分母と分子の確率をそれぞれ求めさえすればよいのです．
なお，分子の $P(E\cap F)$ では，3回以前に $O$ に戻ることはないことに注意しましょう．
⑧において， 分母の $P(E)$，および分子の $P(E\cap F)$ は，いずれもで述べたように
\begin{align*}
「順序の個数」×「各々の推移の確率」
\end{align*}
によって求まります． そして，事象 $E\cap F$ は事象 $E$ の一部分ですから，「各々の推移の確率」(解答の $p$)は，両者共通です．したがって，⑧のように比をとると $p$ は約分されて消えてしまうので，$p$ の値を求める必要はなく，⑥，⑦のように「順序の個数」のみ求めればよい訳です．
参考までに $p$を求めると，④と⑤より
\begin{align*}
p=1\cdot \left(\dfrac16\cdot 1\right)^2\left(\dfrac56\right)^{n-6}\cdot \dfrac16
\end{align*}
となります．
入試において「条件付き確率」が出題される際には，「・・・であるとき～～である条件付き確率」と明示せず，単に「・・・であるとき～～である確率」としか書かれないこともよくありますから注意してください．
本問は，(1)～(4)の設問に分かれていますが，前の設問を利用するにあたって，「結果」をそのまま用いるのではなく，「考え方」を利用して徐々にステップアップしています．入試でも，このような設問形式になっていることもあります．
本項目は，数列(数学B)に習熟した人向けの内容です．
本問とはちがい，途中経過を考慮せず「$n$ 回後にPが原点Oにある」確率 $p_n$ を求めてみましょう．「途中経過を考慮しない」ということは，「途中経過が多岐に渡り複雑」なので，$p_n$ を本問のように直接求めるのは困難です．そこで，(数学的な意味での)帰納的アプローチ，つまり漸化式を利用する方法を採用します．
