＜方針＞ (1)では，T を行った後の箱 A の状態を地道に素直に把握すればOKです．ところが(2)では，玉の個数，T を行う回数とも増えるので，(1)と同じ作業が実行困難となります．そこで，(1)とはまったく異なる『視点』で考えます．

---

【解答】

(1) 赤玉を R，白玉を W で表し，$\frac{A の玉}{B の玉}$ と書く．
最後に A から赤玉 2 個が選ばれる確率を求めるので，T を 1 回行った後，A に 2 個以上の赤玉があるような事象の推移を考えると，次図のようになる(数値は確率)．

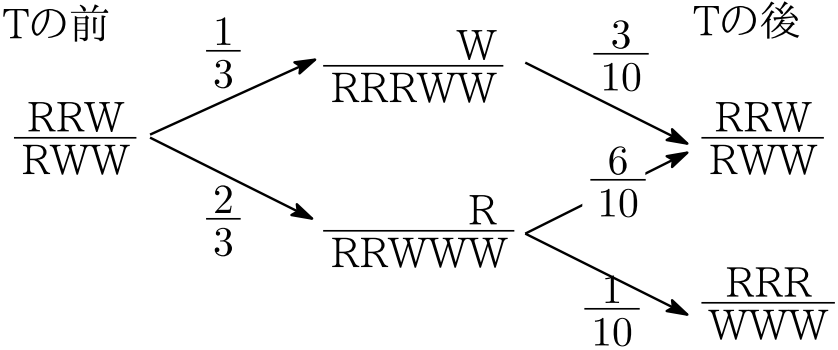
よって，最後に赤玉 2 個を選ぶ確率は

(2) (ある特定の赤玉に注目し，それが入っている箱の推移を考えます．)
$\circ$ A の中にある特定の赤玉1つが入っている箱は，T を1回行うとき次図の確率で推移する．

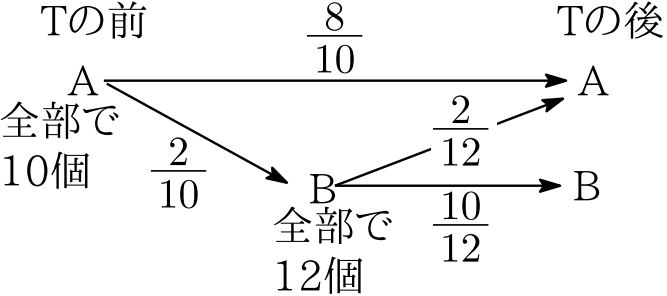
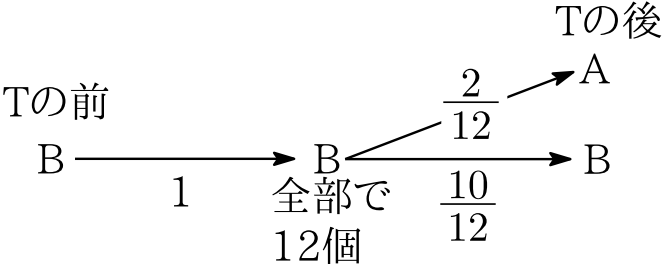
$\circ$ 以下，A の中にある特定の赤玉1つが T を1回行ったとき B の中にあることを「A→B」と表す(他の推移も同様に表す)．上図より各推移の確率は \begin{align} P(\cdots A→\cdots A)=&\frac{8}{10}+\frac{2}{10}\cdot \frac{2}{12}=\frac56, \cdots②\\ P(\cdots A→\cdots B)=&\frac{2}{10}\cdot \frac{10}{12}=\frac16. \cdots②' \end{align} $\circ$ 同様に，次のようになる． \begin{align} P(\cdots B→\cdots A)=&\frac{2}{12}=\frac16， \cdots③\\ P(\cdots B→\cdots B)=&\frac{10}{12}=\frac56. \cdots③' \end{align} $\circ$ 以上をまとめると，ある特定の赤玉1つが入っている箱は次図の確率で推移する．
$\circ$ 最初 A に入っていた赤玉を$\cdots R_1,\cdots R_2,\cdots R_3,\cdots R_4,\cdots R_5$，最初 B に入っていた赤玉を$\cdots R_6,\cdots R_7,\cdots R_8,\cdots R_9$と区別する．
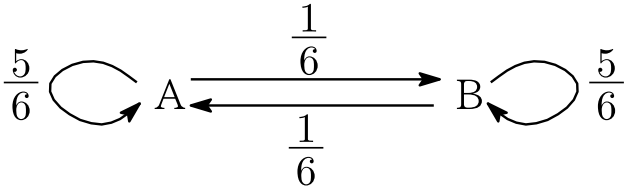
T を2回行った後 $\cdots R_1$ が A にある確率は， \begin{align} &P(\cdots A→\cdots A→\cdots A)+P(\cdots A→\cdots B→\cdots A)\\ =&\frac56\cdot \frac56+\frac16\cdot \frac16=\frac{26}{36}.\\ &(\cdots R_2,\cdots R_3,\cdots R_4,\cdots R_5も同様.) \end{align} T を2回行った後$\cdots R_6$がAの中にある確率は， \begin{align} &P(\cdots B→\cdots A→\cdots A)+P(\cdots B→\cdots B→\cdots A)\\ =&\frac16\cdot \frac56+\frac56\cdot \frac16=\frac{10}{36}.\\ &(\cdots R_7,\cdots R_8,\cdots R_9も同様.) \end{align} $\circ$ $\cdots R_1$が最後に選ばれるのは，T を2回行ったとき$\cdots R_1$が A にあり，かつそこにある10個から $\cdots R_1$ が選ばれるときである．$\cdots R_2,\cdots R_3,\cdots,\cdots R_9$ についても同様であり，これら各々が最後に選ばれる 9 個の事象は排反だから，求める確率は \begin{align} &5\times\frac{26}{36}\cdot \frac1{10}+4\times\frac{10}{36}\cdot \frac1{10}\\ =&\frac{\boxed{17}}{\boxed{36}}. \cdots エオカキ \end{align}

---

【解説】

【解答】にあるような図を用いて事象の推移を視覚的に捉えることは，「確率」（および「場合の数」）の問題を確実に正解するための最良の手段です．

(1)は箱の中にある玉全体の推移を考えました．そのおかげで，最後に赤玉を選ぶ確率を，①のように A の中にある赤玉の個数に応じて求めることができましたね．
それに対して(2)では玉の個数が増え，A の中にある赤玉の個数が $0,1,2,\cdots,9$ と10通りも考えられ，しかも操作 T を2回繰り返すので・・・もう訳が分からなくなりますね．そこで，発想・視点の転換を行います．(1)のように箱の中にある玉全体を考えるのが厳しいので，個々の赤玉に注目して「その1つの玉」の推移“だけ”を追いかけます．その際には，他の玉に関してはもう色すら考えず，単に箱に何個の玉があるか，「その1つの玉」が取り出される確率はいくらか，と考えます．これによって思考が単純化され，処理可能となったのです．

このような「視点の移動」「発想の転換」が有効な問題例を挙げておきます．

---

【類題】 $p$ は正で1未満の定数とする．最初，5枚のコインが表を上にして置かれている．これらのコインに対して次の操作 T を行う．
(1) T を 1 回行ったとき，ちょうど 2 枚が表を上にしている確率を求めよ．
(2) T を 3 回繰り返し行ったとき，ちょうど 2 枚が表を上にしている確率を求めよ．

---

〔解答〕
5枚のコインに $1,2,3,4,5$ と番号を付けて区別する．T を1回行うとき，コインの状態は次の確率で推移する．
(1) 求めるものは， \begin{align} 5枚 \left\{ \begin{array}{l} 表→表\cdots 2枚,\\[-1mm] 表→裏\cdots 3枚 \end{array} \right. \end{align} となる確率であり， \begin{align} _5\cdots C_2p^2(1-p)^3=10p^2(1-p)^3. \end{align} (2) (“時系列”で考えて1回後に何枚表，2回後に何枚表，・・・とやると大変そう！そこで・・・)
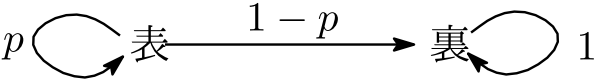
3回後に1番のコインが表である確率 $q$ を求める．一度裏になったらそれ以降も裏のままであることに注意すると，$q$ は3回連続して「表→表」となる確率だから \begin{align} q=p^3. \end{align} 他のコインについても同様であり，3回後の各コインの状態は次のとおり： \begin{align} \left\{ \begin{array}{l} 表\cdots 確率\ p^3,\\[-1mm] 裏\cdots 確率\ 1-p^3. \end{array} \right. \end{align} よって3回後に \begin{align} 5枚 \left\{ \begin{array}{l} 表\cdots 2枚,\\ 裏\cdots 3枚 \end{array} \right. \end{align} となる確率は \begin{align} _5\cdots C_2\left(p^3\right)^2(1-p^3)^3=&10p^6(1-p^3)^3. \end{align} ここでも，(1)は5枚全体の中での表，裏の枚数に注目して解決しますが，(2)ではまず個々のコインについて考察することが重要です．

? のような方針が有効であったのは，(2)で最後に選ぶ玉が「1個」であるからです．赤玉$\cdots R_1,\cdots R_2,\cdots R_3,\cdots R_4,\cdots R_5$および$\cdots R_6,\cdots R_7,\cdots R_8,\cdots R_9$の各々が最後に選ばれる事象が，全て「排反」(同時には起こらない)おかげで，単純にこれらの確率を加えることで答が得られたわけです．

(1)で最後に選ぶ玉が1個なら，(2)と同様に次のように求まります．立式と結果のみ記しておきますから，各自考えてみてください． \begin{align} &2\times\left(\frac13+\frac23\cdot \frac25\right)\cdot \frac13+1\times\frac25\cdot \frac13\\ =&\frac8{15}. \end{align} 「スマホで読むだけでわかるようにして！」と思ってるアナタ．甘え過ぎです．(笑)

(1)の〔図1〕に記された確率のうち \begin{align} \frac{\cdots R\cdots R\cdots W}{\cdots R\cdots W\cdots W}\longrightarrow\frac{\phantom{\cdots R\cdots R\cdots R\cdots W}\cdots W}{\cdots R\cdots R\cdots R\cdots W\cdots W} の確率\frac13\,. \end{align} について解説しておきます．玉を全て区別して考えると，箱 A の「$\cdots R\cdots R\cdots W$」から取り出す2個の組合せ：$_3\cdots C_2=3$通りの各々は等確率(同様に確からしい)．そのうち R 2個である組合せは1通り．よってこの確率は$\displaystyle\frac13$．あるいは，取り出されない1個に注目し，それが W である確率として求めることもできますね．(〔図1〕にある他の推移の確率も同様です．)

(2)で，A の中にある特定の赤玉1つが，T を行うとき取り出されて B に移される2個に含まれる確率$\displaystyle\frac{2}{10}$の求め方は，次のとおりです．
〔解法1〕取り出す2個の組合せ：$_{10}\cdots C_2$通りの各々は等確率．そのうち特定の赤玉を含む組合せは，他の1個を考えて9通り．よってこの確率は \begin{align} _{10}\cdots C_2=\frac{9\cdot 2}{10\cdot 9}=\frac{2}{10}. \end{align} 〔解法2〕A の玉$10$個全てをでたらめに1列に並べ，左から$1$番目と$2$番目を選ぶと考える．特定の玉が$2$番目までに並ぶ確率を考えて，この確率は $ \displaystyle\frac{2}{10}. $ (2)の〔図2〕，〔図3〕にある推移確率 $\displaystyle\frac2{12}$なども同様です．

解答(2)の②,②$'$は，互いに余事象の関係にある事象の確率ですから，一方を求めれば他方はそれを「1」から引くことによっても求められます．ですが，「確率」というのはミスを犯しやすい分野ですから，両方とも求めてみて，それらの和が1になるかどうか確かめる方が賢明といえます．(もちろん，③と③$'$についても同様です．)

(2)において，A から玉を1個選ぶときそれが赤である確率は，T を行う前の段階では$\displaystyle\frac5{10}=\frac12$でしたが，本問の結果からわかるように T を2回行った後では$\displaystyle\frac{17}{36}\left(<\frac{18}{36}=\frac12\right)$となり，少し減少しました．これは，初めの状態において A より赤の比率が少ない B と玉の入れ替えを行ったため，A にある赤玉の個数が半分より少なくなる可能性が高まったためだと考えられます．

この項目は(2)に関する補足事項で，数学B「数列」に習熟し，いわゆる「確率漸化式」について学習したことのある人限定の内容です．
最初 A にあった赤玉 $\cdots R_1$が，T を $n$ 回繰り返した後 A に入っている確率を $p_n$とする．$(\cdots R_2,\cdots R_3,\cdots R_4,\cdots R_5も同様.)$〔図4〕より \begin{align} p_{n+1}=&p_n\cdot \frac56+\left(1-p_n\right)\cdot \frac16\\ =&\frac23p_n+\frac16. \cdots④ \end{align} また，最初( T を「0回」行った後) $\cdots R_1$は A にあったから \begin{align} p_0=&1. \cdots⑤ \end{align} ④を変形すると \begin{align} &p_{n+1}-\frac12=\frac23\left(p_n-\frac12\right).\\ \therefore\ &p_n-\frac12=\left(p_0-\frac12\right)\left(\frac23\right)^n. \end{align} これと⑤より \begin{align} p_n=\frac12+\frac12\left(\frac23\right)^n. \cdots⑥ \end{align} (2)の〔図4〕からわかるように，T を $n$ 回繰り返した後，最初 B にあった赤玉 $\cdots R_6$ が B に入っている確率もこれに等しいから，$\cdots R_6$ が A に入っている確率は $1-p_n$．$(\cdots R_7,\cdots R_8,\cdots R_9も同様.)$
以上より，T を $n$ 回繰り返した後で A から1個を選ぶとき，それが赤である確率 $q_n$ は \begin{align} q_n=&5\cdot p_n\cdot \frac1{10}+4\cdot \left(1-p_n\right)\cdot \frac1{10}\\ =&\frac1{10}p_n+\frac25\\ =&\frac1{10}\left\{\frac12+\frac12\left(\frac23\right)^n\right\}+\frac25\\ =&\frac9{20}+\frac1{20}\left(\frac23\right)^n. \cdots⑦ \end{align} 試しに $n$ に 2 を代入してみると \begin{align} q_2=&\frac9{20}+\frac1{20}\left(\frac23\right)^2\\ =&\frac9{20}+\frac1{20}\cdot \frac49\\ =&\frac{81+4}{20\cdot 9}=\frac{17}{36} \end{align} となり，本問(2)の答と確かに一致していますね．
また，⑦において，$n$ が大きくなるにつれて $\displaystyle\left(\frac23\right)^n$ は小さくなって 0 に近づいていきます．つまり，T を行う回数が多くなるほど最後に赤が選ばれる確率は減少していき，$\displaystyle\frac9{20}$ に近づきます．(数学Ⅲでは，このことを $\displaystyle\lim_{n\to\infty}q_n=\frac9{20}$ と表します．)玉の入れ替え T を何度も繰り返すと，最初 A，B どちらの箱に赤が何個入っていたかの影響は薄れ，最後に赤玉が選ばれる確率は，A，B 合わせた全体における赤の個数 9 個と玉の総数 20 個の比に近づいていくわけです．
同じようなことが⑥式にも表れています．$p_n$ は $n$ を大きくしていくと $\displaystyle\frac12$ に近づきます．A の中にあった特定の赤玉1つは，T を繰り返すと最初 A にあったことの影響が薄れ，A，B にほぼ均等な確率で入っていることになるのですね．